ECUACIÓN DE BERNOULLI

 Principio de Bernoulli 

Daniel Bernoulli, matematico, tomada de
 https://upload.wikimedia.org/wikipedia/commons/b/b3/ETH-
BIB-Bernoulli%2C_Daniel_%281700-1782%29-Portrait-Portr_10971.tif_%28cropped%29.jpg

Se utiliza para analizar un fluido que fluye de arriba abajo a través de toda clase de tubos, por lo que se le puede considerar una declaración del principio de la conservación de la energía para el flujo de fluidos es el descenso de presión de un líquido por un estrechamiento de una vía de flujo.

Para poder entender mejor la ecuación de Bernoulli es necesario saber sobre su principio el cual dice que en ciertos puntos a lo largo de una línea horizontal de flujo, las regiones de mayor presión tienen una menor velocidad del fluido, y las regiones de menor presión tienen una mayor velocidad del fluido. Este principio es otra forma de decir que el agua irá más rápido si hay más presión detrás de ella que delante de ella.

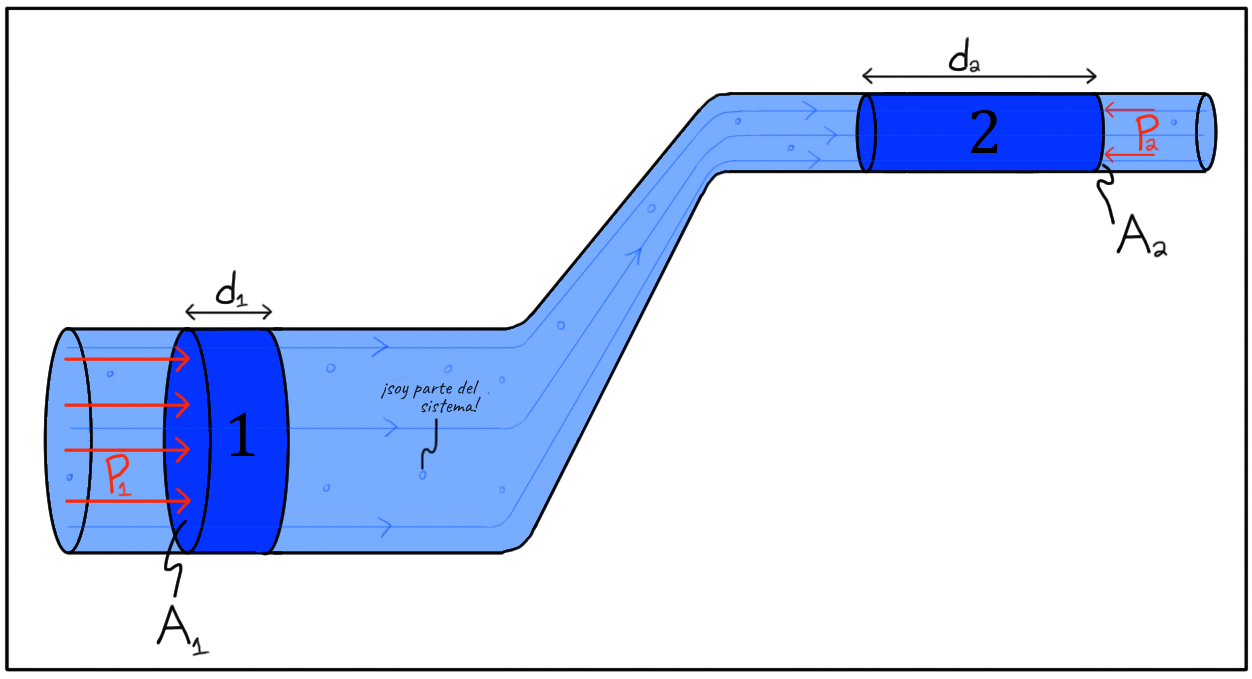
Sabemos que  el agua debe acelerar esto debido a la ecuación de continuidad, por lo que una cantidad neta positiva de trabajo será mas grande que la otra cantidad de trabajo. Esto quiere decir que la presión en el lado ancho y lento (p1) tiene que ser mayor a la presión del lado angosto y rápido (p2).

Demostración de la Ecuación de Bernoulli tomada de https://cdn.kastatic.org/ka-perseus-images/2d10eae03f6e152de6a8270420d5298b31099856.png

A todo esto se le llama: 💧Principio de Bernoulli💧

Una vez explicado esto entendemos que la ecuación de Bernoulli es esencialmente una manera matemática de expresar el principio de Bernoulli de forma general, tomando en cuenta los cambios en las energías potenciales debidas a la gravedad.

La ecuación de Bernoulli relaciona la presión, la velocidad y la altura de dos puntos cualquiera en un fluido con flujo laminar constante de densidad.

Ecuación de Bernoulli tomada de https://i0.wp.com/cursoparalaunam.com/wp-content/uploads/2021/01/FORMULA-DE-LA-ECUACION-DE-BERNOULLI-1.jpg?resize=469%2C144&ssl=1

Para usar la ecuación de Bernoulli se tiene que seleccionar uno de los puntos en donde se quiere determinar la variable desconocida.

Los términos 1/2​ρv2 y ρgh en la ecuación de Bernoulli se parecen a la energía cinética ½ mv2 y la energía potencial mgh. Considerando esto se derivara la ecuación de Bernoulli por medio de la conservación de la energía.

Demostración del principio de Bernoulli tomada de https://cdn.kastatic.org/ka-perseus-images/9e48e4ce97bc817f78f76f6cfb4129183656f848.png